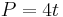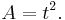Square (geometry)

Square
A square is a regular quadrilateral.
Families	2-hypercube, 2-orthoplex
Edges and vertices	4
Schläfli symbol	{4}
Coxeter–Dynkin diagrams
Symmetry group	Dihedral (D4)
Area (with t=edge length)	t2
Internal angle (degrees)	90°
Properties	convex, cyclic, equilateral, isogonal, isotoxal

In geometry, a square is a regular quadrilateral. This means that it has four equal sides and four equal angles (90 degree angles, or right angles). A square with vertices ABCD would be denoted ABCD.

Perimeter and area

The area of a square is the product of the length of its sides.

The perimeter of a square whose sides have length t is

and the area is

In classical times, the second power was described in terms of the area of a square, as in the above formula. This led to the use of the term square to mean raising to the second power.

Standard coordinates

The coordinates for the vertices of a square centered at the origin and with side length 2 are (±1, ±1), while the interior of the same consists of all points (x₀, x₁) with −1 < x_i < 1.

Construction of a square using a compass and straightedge.

Equations

The equation max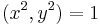 describes a square. This means " 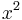or 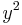, whichever is larger, equals 1." The circumradius of this square is .

Properties

A square is both a rhombus (equal sides) and a rectangle (equal angles) and therefore has all the properties of both these shapes, namely:

• The diagonals of a square bisect each other
• The diagonals of a square bisect its angles.
• The diagonals of a square are perpendicular.
• Opposite sides of a square are both parallel and equal.
• All four angles of a square are equal. (Each is 360/4 = 90 degrees, so every angle of a square is a right angle.)
• The diagonals of a square are equal.

Other facts

• If the diagonals of a rhombus are equal, then that rhombus must be a square. The diagonals of a square are (about 1.414) times the length of a side of the square. This value, known as Pythagoras’ constant, was the first number proven to be irrational.
• A square can also be defined as a rectangle with all sides equal, or a rhombus with all angles equal, or a parallelogram with equal diagonals that bisect the angles.
• If a figure is both a rectangle (right angles) and a rhombus (equal edge lengths), then it is a square. (Rectangle (four equal angles) + Rhombus (four equal sides) = Square)
• If a circle is circumscribed around a square, the area of the circle is 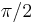(about 1.57) times the area of the square.
• If a circle is inscribed in the square, the area of the circle is (about 0.79) times the area of the square.
• A square has a larger area than any other quadrilateral with the same perimeter ([1]).
• A square tiling is one of three regular tilings of the plane (the others are the equilateral triangle and the regular hexagon).
• The square is in two families of polytopes in two dimensions: hypercube and the cross polytope. The Schläfli symbol for the square is {4}.
• The square is a highly symmetric object (in Goldman geometry). There are four lines of reflectional symmetry and it has rotational symmetry of order 4 (through 90°, 180° and 270°). Its symmetry group is the dihedral group D₄.

Non-Euclidean geometry

In non-euclidean geometry, squares are more generally polygons with 4 equal sides and equal angles.

In spherical geometry, a square is a polygon whose edges are great circle arcs of equal distance, which meet at equal angles. Unlike the square of plane geometry, the angles of such a square are larger than a right angle.

In hyperbolic geometry, squares with right angles do not exist. Rather, squares in hyperbolic geometry have angles of less than right angles. Larger squares have smaller angles.

Examples:

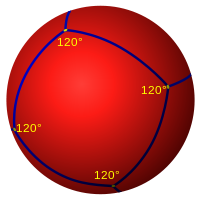Six squares can tile the sphere with 3 squares around each vertex and 120 degree internal angles. This is called a spherical cube. The Schläfli symbol is {4,3}.

Squares can tile the Euclidean plane with 4 around each vertex, with each square having an internal angle of 90 degrees. The Schläfli symbol is {4,4}.

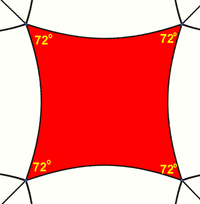Squares can tile the hyperbolic plane with 5 around each vertex, with each square having 72 degree internal angles. The Schläfli symbol is {4,5}.

Graphs

The K₄ complete graph is often drawn as a square with all 6 edges connected. This graph also represents an orthographic projection of the 4 vertices and 6 edges of the regular 3-simplex (tetrahedron).

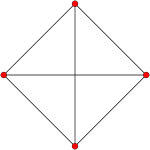3-simplex (3D)

See also

• Cube
• Pythagorean theorem
• Square lattice
• Unit square
• Squircle
• Hypercubes family
  • Point (geometry) - -
  • Line (geometry) - {}
  • Square - {4}
  • Cube - {4,3}
  • Tesseract - {4,3,3}
  • Penteract - {4,3,3,3}
  • Hexeract - {4,3,3,3,3}
  • Hepteract - {4,3,3,3,3,3}
  • Octeract - {4,3,3,3,3,3,3}
  • Enneract - {4,3,3,3,3,3,3,3}
  • Dekeract - {4,3,3,3,3,3,3,3,3}
  • Hendekeract - {4,3,3,3,3,3,3,3,3,3}
  • Dodekeract - {4,3,3,3,3,3,3,3,3,3,3}
  • n-eract

External links

• Animated course (Construction, Circumference, Area)
• Weisstein, Eric W., "Square" from MathWorld.
• Definition and properties of a square With interactive applet
• Animated applet illustrating the area of a square